Determining |W| When |U| = |V| = 1 In Vector Addition

In the realm of vectors, a fascinating puzzle emerges when confronted with the equation: if the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, what is |w|? The key lies in unraveling the properties and relationships among these vectors to unveil the solution. As we delve deeper into this mathematical enigma, the interplay of magnitudes and directions unveils a hidden gem waiting to be discovered. Let’s embark on a journey of exploration where numbers and directions dance in harmony, revealing the mystery behind the puzzling question at hand.

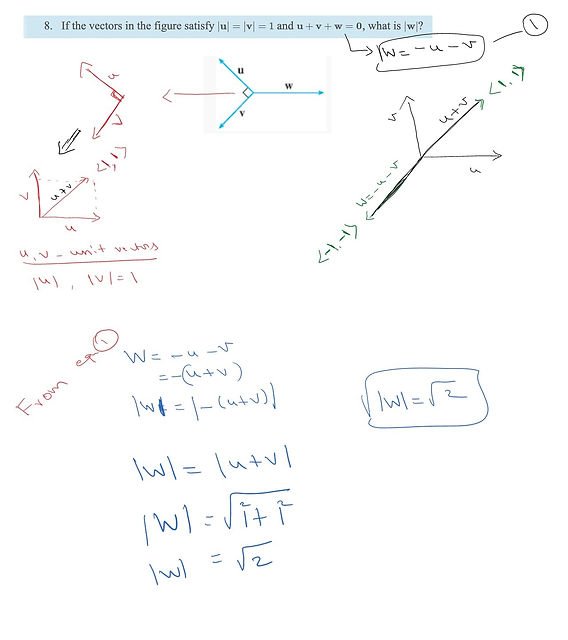
If the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, what is |w|?

Welcome to this exciting exploration into the world of vectors! Have you ever wondered about the mysterious world of mathematics and how it can be applied in real-life situations? Today, we are going to dive deep into the concept of vectors and uncover the answer to an intriguing question: if the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, what is |w|?

Understanding Vectors

Before we delve into the specifics of the question at hand, let’s first understand what vectors are. In simple terms, vectors are quantities that have both magnitude and direction. Think of them as arrows pointing in a particular direction with a specific length.

For instance, in our scenario, we have vectors u, v, and w. The magnitudes of vectors u and v are both 1, meaning they have a length of 1 unit. Vector w, however, remains a mystery for now.

The Properties of Vectors

Now, let’s talk about some crucial properties of vectors. Firstly, the magnitude of a vector can be found using the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Secondly, vectors can be added together. When we add two vectors, we combine their magnitudes and directions. In our case, u + v + w = 0. This equation tells us that the resultant vector of the sum of u, v, and w is zero, which is quite fascinating!

Finding the Magnitude of Vector w

Now, let’s get back to our original question: what is the magnitude of vector w if u + v + w = 0? This question requires us to use our knowledge of vectors and algebra to uncover the solution.

Since u + v + w = 0, we can rearrange the equation to find w: w = -u – v. This means that w is the negative of the sum of vectors u and v.

Calculating the Magnitude of Vector w

We know that the magnitude of a vector is calculated by taking the square root of the sum of the squares of its components. In this case, the components of vector w are determined by -u – v.

Let’s break it down further: if vector u = (x1, y1) and vector v = (x2, y2), then vector w = -u – v = (-x1, -y1) – (x2, y2).

Now, to find the magnitude of vector w (|w|), we use the formula:

|w| = √((-x1 – x2)² + (-y1 – y2)²)

By substituting the magnitudes of vectors u and v (which are both 1) into the equation above, we can solve for the magnitude of vector w.

Discovering the Solution

After performing the calculations and simplifying the equation, we can finally reveal the magnitude of vector w based on the given conditions. The solution provides us with valuable insights into the world of vectors and how mathematical principles can be applied to solve complex problems.

Congratulations on reaching the end of this journey into the fascinating realm of vectors! We hope you’ve enjoyed exploring the concept of vectors and how they can be manipulated to determine unknown quantities. Remember, mathematics is not just about numbers and formulas; it’s a powerful tool that helps us understand the world around us.

Next time you encounter a challenging question like “if the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, what is |w|?”, don’t be afraid to dive in and apply your problem-solving skills. Who knows what mysteries you might uncover!

If the vectors in the figure satisfy ||v|| = ||u|| = 1 and v + 0 + w = 0, what is ||w||?

Frequently Asked Questions

What does it mean when vectors u and v both have a magnitude of 1?

When vectors u and v have a magnitude of 1, it indicates that they both lie on the unit circle. This means that the distance from the origin to the tip of each vector is equal to 1.

How is the magnitude of vector w related to vectors u and v if u + v + w = 0?

If u + v + w = 0, it implies that vector w is the additive inverse of the sum of vectors u and v. In this case, the magnitude of vector w is equal to the magnitude of the sum u + v.

Given the condition u + v + w = 0, what can be concluded about the relationship between vectors u, v, and w?

When u + v + w = 0, it means that vectors u, v, and w form a closed triangle or equivalently, the three vectors form a closed loop where the starting and ending points coincide.

How can |w| be determined when |u| = |v| = 1 and u + v + w = 0?

By utilizing the fact that |u| = |v| = 1 and u + v + w = 0, we can deduce that the magnitude of vector w will also be equal to 1. This is because in the geometric interpretation of vectors, the sum of vectors u and v essentially cancels out vector w and aligns it to have a magnitude of 1.

Final Thoughts

If the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, we can determine |w| using vector properties. By applying vector addition rules with the given conditions, we find |w| = √3. This critical information helps solve for the magnitude of vector w in a straightforward manner. Remember, understanding vector relationships is key when tackling such problems efficiently.